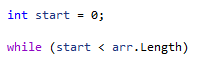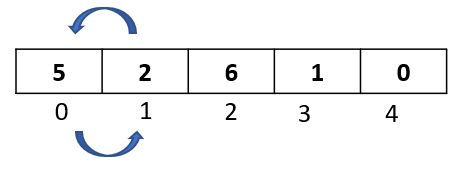We have already established the importance of sorting algorithms in computer science in the previous posts on Bubble and Selection sorts. Let’s continue our journey with another such algorithm: Insertion Sort.
Definition
Insertion sort works on the array data structure as follows:
- Start from the second element in the array, and iterate till the last element
- In each iteration, select an element, and compare this element with all the elements to its left.
- While comparing, whenever we find a greater element than our selected element, we move the greater element one step to the right
- At the end of each iteration, we find a vacant spot to insert the element that we selected in the beginning of the iteration.
Let’s look at this visually to get a better understanding.
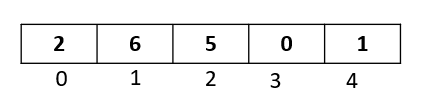
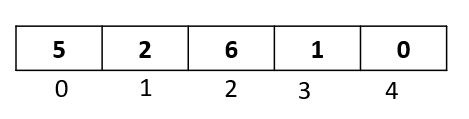
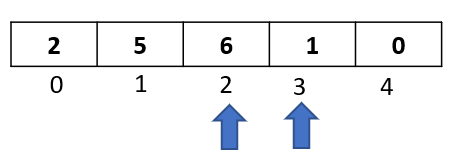
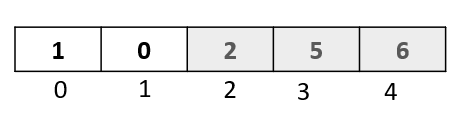
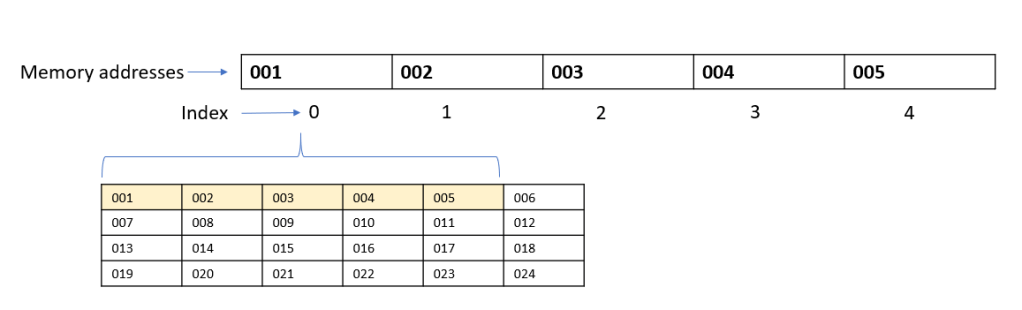
We will be sorting the following array:
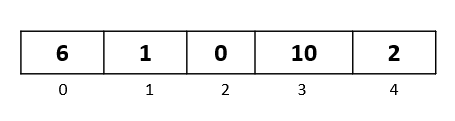
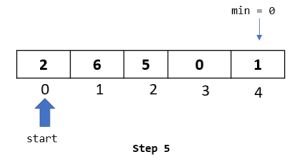
We have five elements from index 0 to index 4.
Passthrough 1
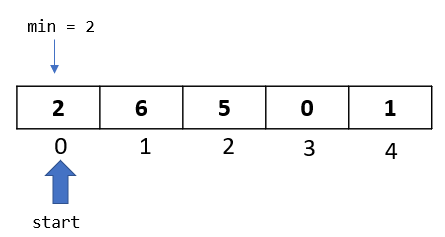
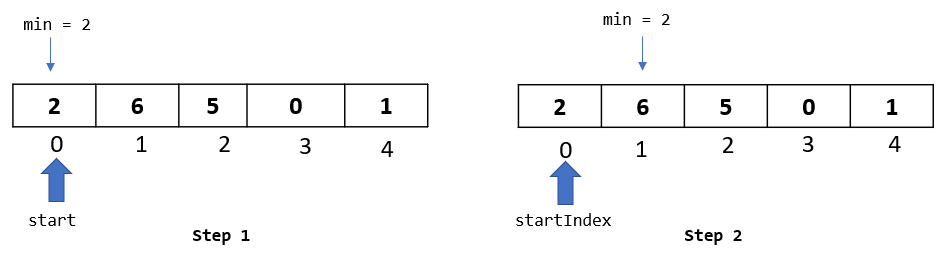
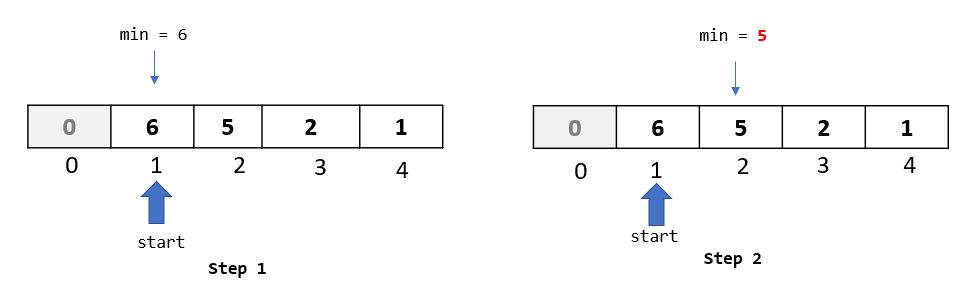
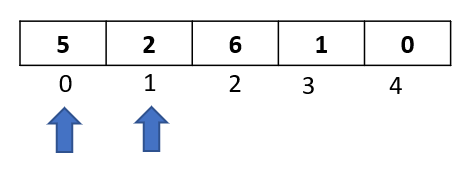
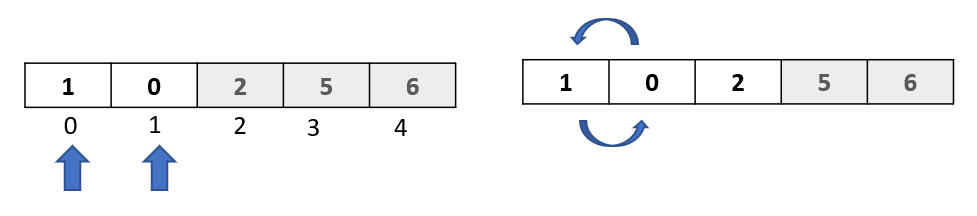
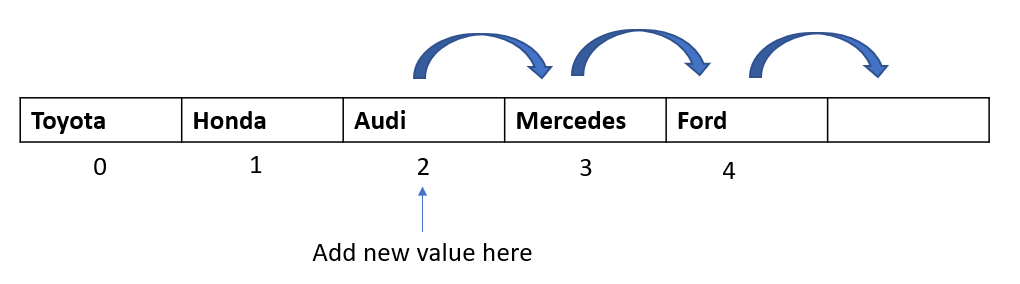
Step 1: The algorithm starts from the second element in the array, so let’s select the element at index 1.

Step 2: Compare the selected element to all the elements to its left. Here we have just 1 element towards the left -> “6” at index 0. Let’s do the comparison: Is 6 greater than 1 ? Yes. Then as per the algorithm, let’s move it one spot to the right:
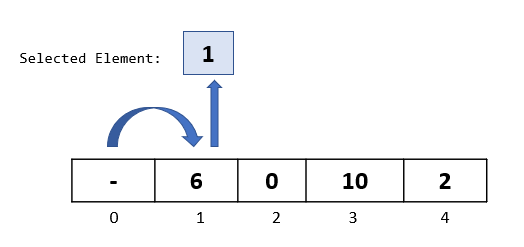
Step 3: Since we had only one element to the left of the selected element, we are done with the comparison and movements for this passthrough. Now we need to find a spot to insert our selected element.
As we can see, the spot at index 0 became available, since we moved the element “6” from index 0 to index 1. So let’s insert our selected element there:
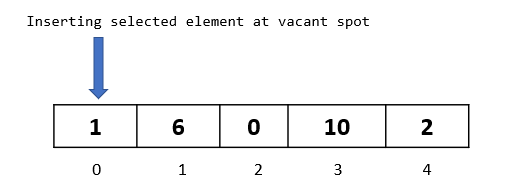
And that concludes our first passthrough.
Passthrough 2
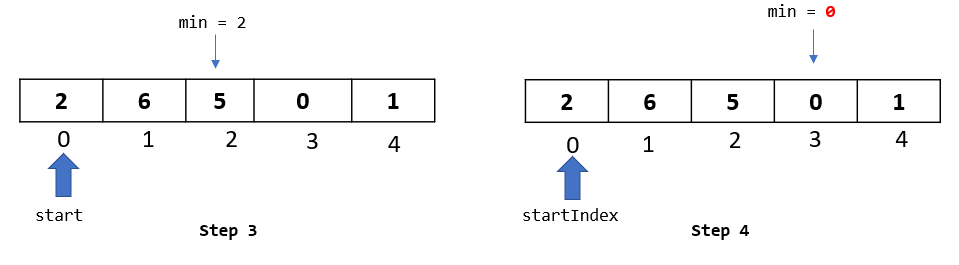
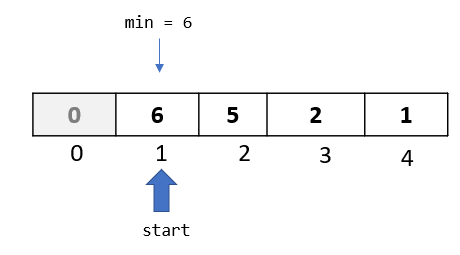
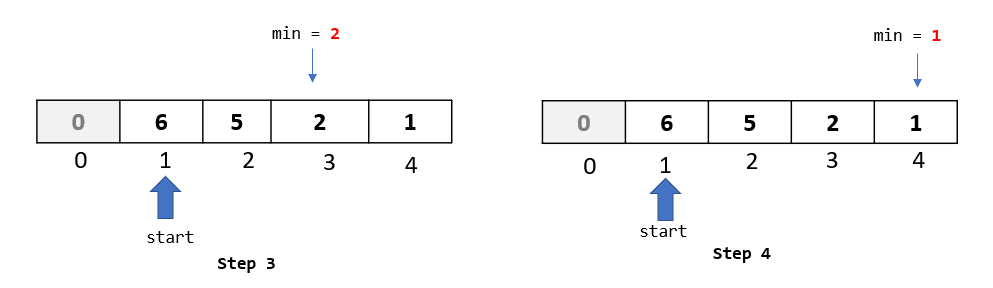
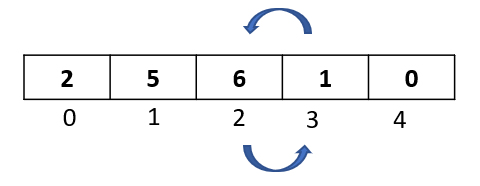
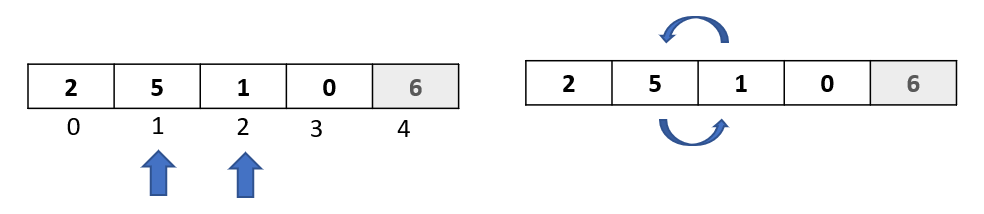
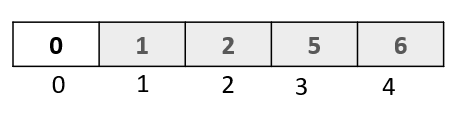
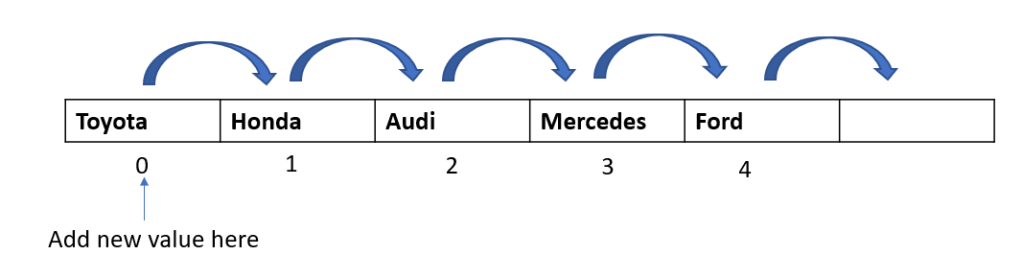
Step 1: In the first passthrough, we selected the element at index 1. In this passthrough, we will move to the next element and select the one at index 2:
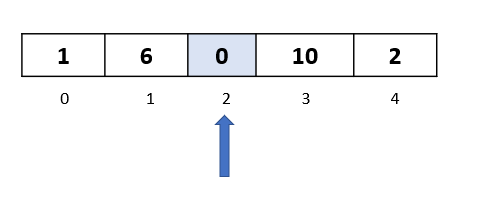
Step 2: We now begin the comparison process where we will compare the selected element to all the elements towards its left.
Compare selected element “0” to “6” ,the first element to its left. Since 6 is greater than 0, we will move it one step to the right
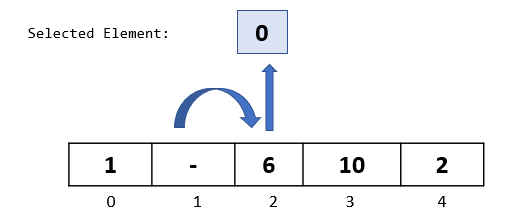
Compare selected element “0” to “1”, the second element to its left. Since 1 is greater than 0, we will move it one step to the right
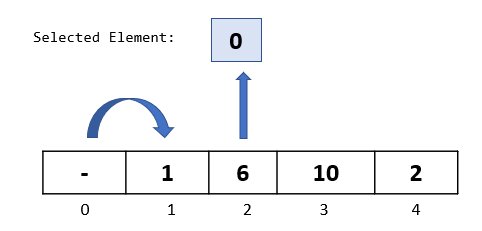
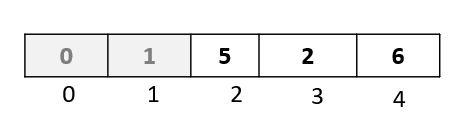
Step 3: We are done with the comparisons and movements for this passthrough. Now is the time to insert our selected element back into the array at the available vacant spot. Since we moved both the elements 1 and 6, we have a vacant spot at index 0. So let’s go ahead and insert our selected element there
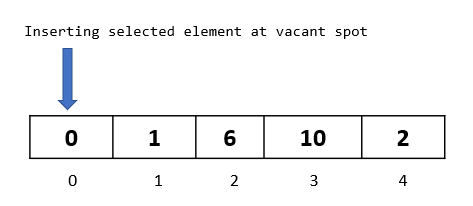
Passthrough 3
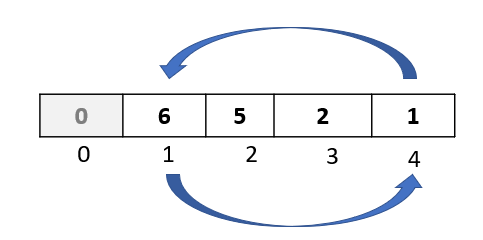
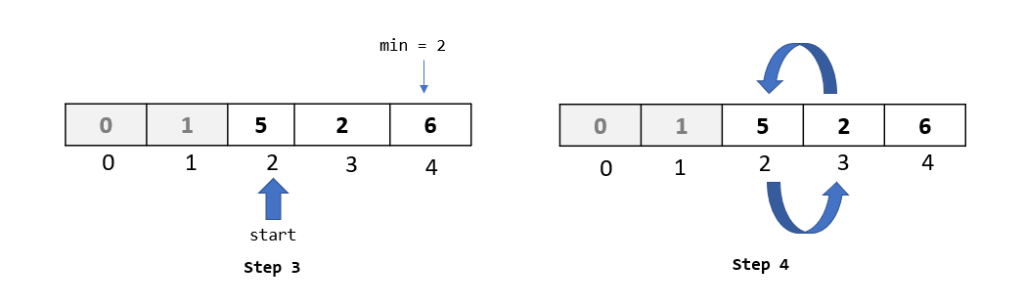
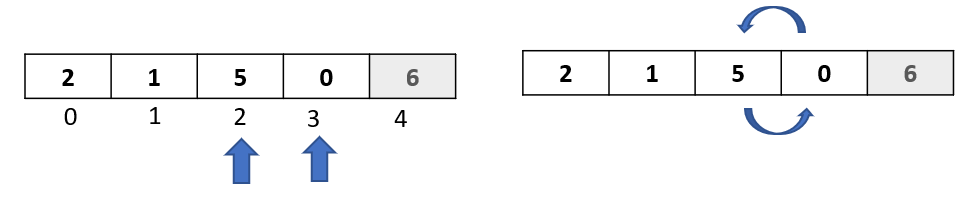
Step 1: Now that we have got a hang of the algorithm , we know that in this passthrough we will select the element at index 3.

Step 2: Let’s begin with our comparisons. We would be comparing our selected element “10” with all the elements to its left.
We do our first comparison with element “6”. Since “6” is not greater than 10, we do not move it to the right.
Also, from our previous passthroughs, we know that all the elements that are to the left of 6 are smaller than 6 (because of all the previous steps that we did). This means that in this passthrough, we do not need to move any element to the right.
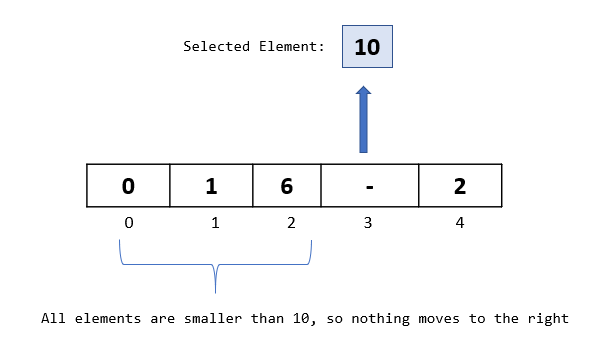
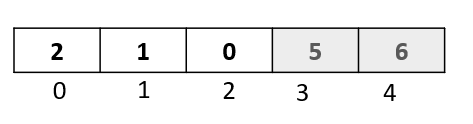
Step 3: We need to insert our selected element to an available spot in the array. Since we moved no element in the last step, the vacant spot would be the same position at which the element was before the passthrough. Hence, we put the element back at that position, and move on to the next passthrough.
Passthrough 4
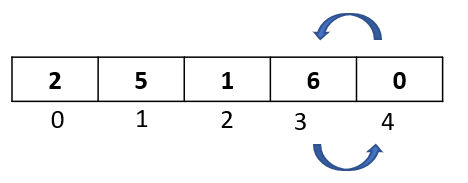
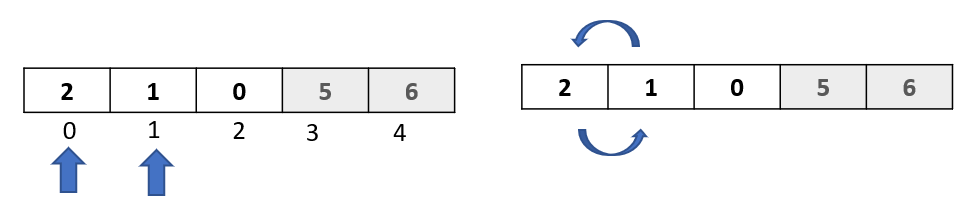
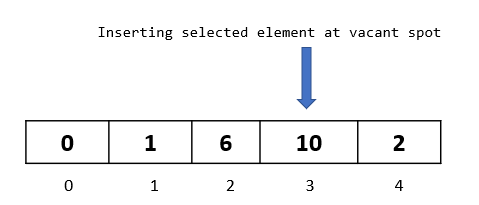
Step 1: We move to the next element in our array, and select the element at index 4. Note that this is the last element in the array, and so this will be our last passthrough
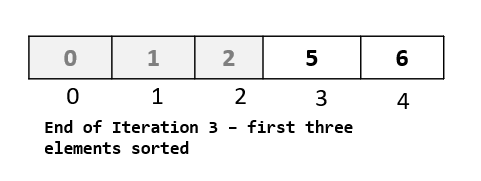
Step 2: We now begin with our comparisons. We need to compare the element “2” with all the elements to its left.
Let’s start with the element at index 3 -> “10”. Since 10 is greater than 2, we move it one step to the right.

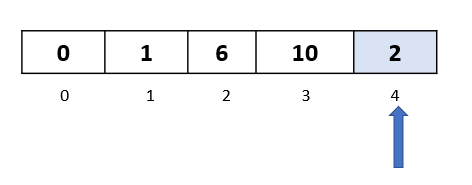
We now compare the selected element “2” with the element at index 2. Since 6 is greater than 2, we move 6 one step to the right
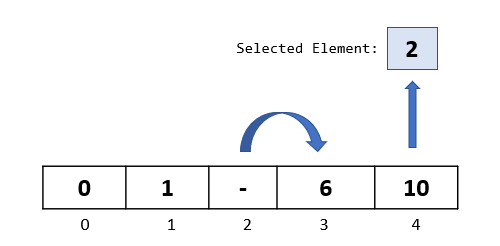
We now compare the selected element “2” with the element at index 1. Since 1 is not greater than 2, we do not move it to the right.
Also, because of our previous passthroughs and steps in the algorithm, we know for sure that all the elements towards the left of “1” would be less than “1”.
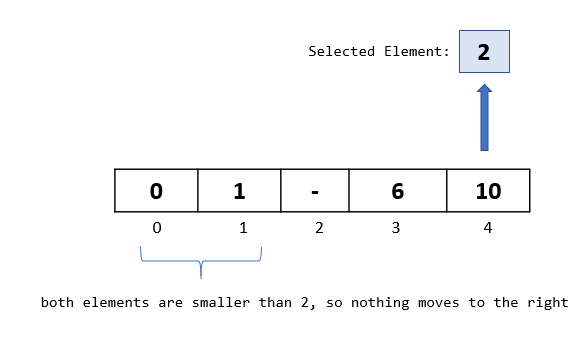
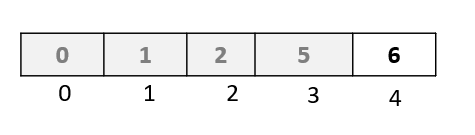
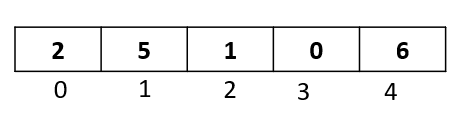
Step 3: After we have completed all the comparisons, we now need to insert our selected element back to the vacant spot in the array. Since we have the spot at index 2 vacant, we insert our selected element at index 2

And with the end of this passthrough, we have sorted our array!
Recap
Insertion sort is a bit tricky to understand as it has a lot of steps, and it compares elements in the other direction (towards the left), as opposed to other “forward looking” algorithms that compare the elements to their right.
So let’s recap what we did once again:
- We did 4 passthroughs for an array of 5 elements
- In each passthrough, we selected one element
- We compared the selected element to all the elements to its left
- Whenever we found an element greater than the selected element, we moved that element to the right
- At the end of all the comparisons and movements, we had one vacant spot available in the array. We inserted our selected element to that spot ending our passthrough.
And hopefully now it makes sense why it is called insertion sort!
Implementation in C#
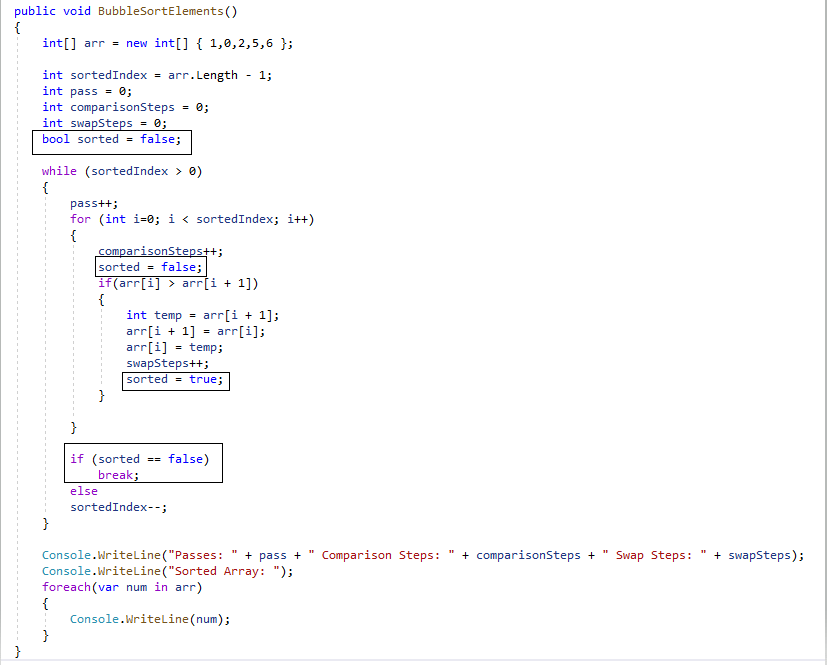
Here is an implementation of the insertion sort algorithm in C#

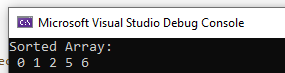
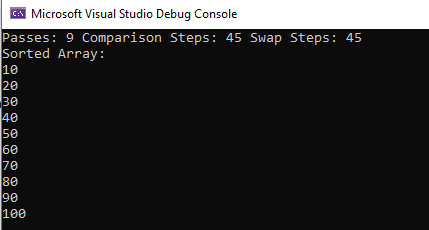
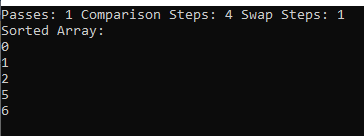
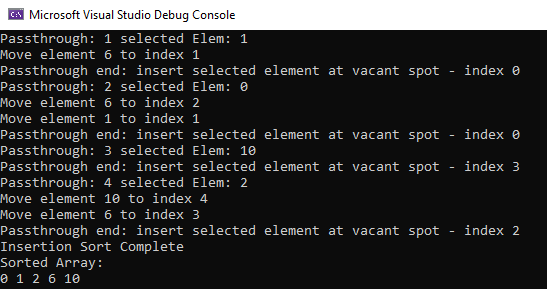
On running the above code, we get the following output:
Growth Complexity Analysis
Before jumping to mathematical terms that involve the variable “N”, let’s first try to look how many operations we performed in our algorithm.
We did the following operations on our array of 5 elements:
- 4 passthroughs
- 1 comparison and 1 movement operation in the first passthrough
- 2 comparison and 2 movement operations in the second passthrough
- 1 comparison and no movement in the third passthrough
- 3 comparisons and 2 movements in the fourth passthrough
- We also did 1 selection and 1 insertion operation in each passthrough, giving us a total of 4 selection and 4 insertion operations
This gives us a total of 4 passthrough + 7 comparisons + 5 movements + 4 selections + 4 insertions
Or a grand total of 24 operations for our array of 5 elements. Which is closer to (5) squared.
Let’s now try and derive a generalized complexity in terms of “N”.
Let’s focus on a worst case scenario – a case where all the elements in the array are in descending order.
For 1 passthrough we will do approximately: 1 selection + 1 insertion + (N-1) comparisons + (N-1) movements
And so for (N-1) passthroughs we would do approximately:
(N-1) * (1 + 1 + (N-1) + (N-1)) operations
If we ignore all the constants, we get something like:
(N) * (N)
which is equal to (N)^2 (n squared) operations
Thus we can say that the worst case complexity of an insertion sort is O(N^2) or order of N squared.
Summary
Insertion sort begins with the second element and iterates the array till the last element. In each iteration or passthrough, we select one element and compare it with the elements to its left. Whenever the elements to the left are greater than the selected element, we move them one step to the right. We then insert our selected element back to the array at the vacant spot.
This whole process would take a time complexity of O(N^2) in a worst case scenario.
feature image source: https://www.pexels.com/@digitalbuggu