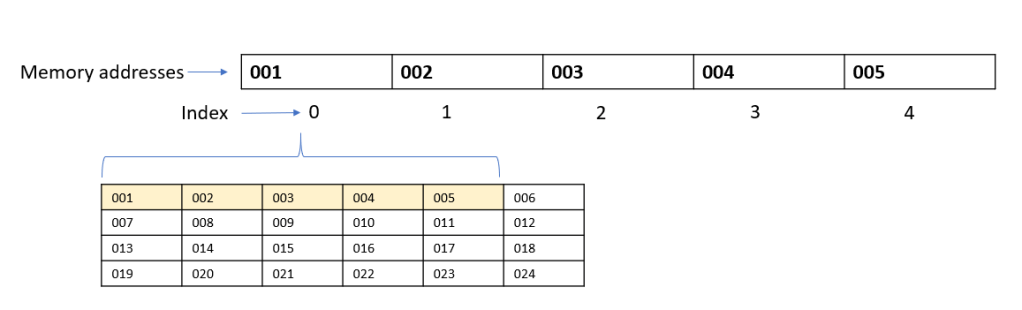
Search can be considered as one of the most essential features that a software product can have for a good user experience. For instance, whenever we log onto amazon, we can directly go to the search bar and enter the product that we wish to buy, rather than going through all the products one by one!
Search algorithms can get really complex as the amount of data increases, and the key to writing efficient algorithms would be to first understand the basics. Today we will look into two simple search algorithms that work on the Array data structure. This will give you a perspective on how search operation is performed and the implications on efficiency when input data is increased.
Linear Search
As the name suggests, linear search goes over all the items in the array, one by one, until we find the desired element.
Let’s say we have the following array which stores a list of products added to an online grocery shopping cart:

At checkout, we decide to remove Soda from the list. Now in order to do that, we would first need to find the exact location of the item “soda” in our list.
A linear search would proceed as follows:
Step 1: Start from index 0. Is the item “Soda” ?

Nope the item is not Soda. Proceed to the next element
Step 2: Is the item at index 1 “Soda”?

Nope. Proceed to the next element
Step 3: Is the item at index 2 “Soda”?

Nope. Proceed to the next element
Step 4: Is the item at index 3 “Soda” ?

Nope. Proceed to the next element
Step 5: Is the item at index 4 “Soda”?

Nope. Proceed to the next element
Step 6: Is the item at index 5 “Soda”?

Yes! Finally! Phew!
The item soda was found at index 5 (or position 6) in the array by our linear search algorithm. In order to find an item at the 6th position, the algorithm took 6 steps. If Soda was present at position 7, then the algorithm would have taken 7 steps. Thus, we can say that Linear search will take n steps for finding an element at nth position. In other words, the complexity of the algorithm is O(n) or order of n.
Implementation in C#
Following is an implementation of the linear search algorithm in C#:
public void LinearSearchProduct()
{
string[] cart = new string[] { "Apples", "Eggs", "Bread",
"Milk", "Yogurt", "Soda", "Cheese", "Rice",
"Beans" };
string item = "Soda";
bool found = false;
//For loop will go over each element of the array
for(int i=0; i < cart.Length; i++)
{
if(cart[i] == item)
{
found = true;
Console.WriteLine("Product found at index: " + i);
break;
}
}
if(found == false)
{
Console.WriteLine("Product not found");
}
}Growth Analysis
In our example, we just had an array of nine elements. Imagine if the array contains thousands of elements. Even worse, imagine if the item that we are interested in is at the last position in the array! Since the linear search algorithm would need to go over the entire array, it would probably not be a great option to use when we have large amounts of data.
As we can see in the table below, for every new element added to the array, Linear search would need one additional step to find an item, following a growth complexity of O(n):
| Number of Elements in Array | Maximum Number of Steps Taken by Linear Search |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
Binary Search
Binary search is a much faster algorithm than linear search. The only caveat is that Binary search expects the data in our array to be sorted. In other words, the binary search algorithm works on ordered arrays. Once we understand how the algorithm works, this will make much more sense.
The algorithm works by eliminating or ignoring half of the elements of the array with every step until we find the desired element.
First, it starts by looking at the middle element of the array. If the item to be searched is equal to the middle element, we get our result.
Else, it checks if the item to be searched is less than or greater than the middle element.
If the item is less than the middle element, then it considers the first half of the array for the next step and ignores the second half.
If the item is greater than the middle element, then it considers the second half of the array and ignores the first half.
Whichever half it chooses, it repeats all the above steps again by checking the middle element and comparing it with the item to be searched.
We do this until we get the desired element.
Let’s go back to our example to visually see how it works:

We want to search for the item “Soda” in the above array.
First step would be to sort this array following natural ordering (ascending order or Alphabetical in case of strings). So the following would be our input array.
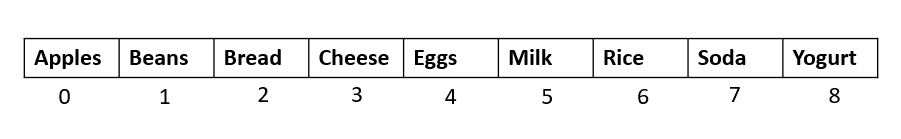
Step 1: Find the middle element of the above array. If the length of the array is n, then the middle element would be n/2 if n is even, and (n+1)/2, if n is odd.
Here, length of array is 9. so our middle element would be at position (9+1)/2 = 5. (This would be index 4, since arrays start from index 0)

Does the middle element = “Soda” ? Nope.
Is “Soda” less than or greater than the middle element? Greater than (Alphabetically Soda comes after Eggs)
Step 2: Select second half of the array and find the new middle element:
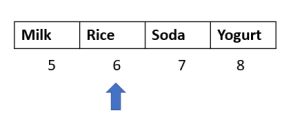
length of this new array is 4, so the middle element would be at the second position (4/2) – here index 6
Does the middle element = “Soda” ? Nope.
Is “Soda” less than or greater than the middle element? Greater than (Alphabetically Soda comes after Rice)
Step 3: Select the second half of the array and find the new middle element:
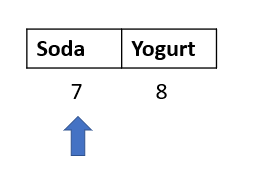
length of this new array is 2, so the middle element would be at the first position (2/2) – here index 7.
Does the middle element = “Soda”? Yes! Return element.
Thus, we can see that the binary search algorithm took only 3 steps to find the desired item.
Growth Analysis
One thing to note is that with every step, the number of elements that we are looking into reduce by half. Let’s look at this from another perspective, that is, for how many new elements would binary search take an additional step?
| Number of Elements in Array | Number of steps taken by binary search | Log representation (to the base 2) |
| 2 | 1 | Log(2) = 1 |
| 4 | 2 | Log(4) = 2 |
| 8 | 3 | Log(8) = 3 |
| 16 | 4 | Log(16) = 4 |
Thus we can see that whenever the elements in the array double, the binary search would take 1 additional step to find the item. This is how the time complexity grows for binary search. Since this growth can be represented in log terms, the complexity of binary search is O(logn) or order of log(n).
Implementation
The implementation of binary search in C# is as follows:
public void BinarySearchProduct()
{
string[] cart = new string[] { "Apples", "Eggs", "Bread",
"Milk", "Yogurt", "Soda", "Cheese", "Rice",
"Beans" };
string item = "Soda";
bool found = false;
//we need to sort cart to implement binary search
Array.Sort(cart);
int start = 0;
int end = cart.Length - 1;
while(start <= end)
{
int len = end - start + 1;
int mid = start + (len / 2);
if (item == cart[mid])
{
Console.WriteLine("Element found at index: " + mid);
found = true;
break;
}
else if (item.CompareTo(cart[mid]) > 0)
{
start = mid + 1;
}
else
{
end = mid - 1;
}
}
if(found == false)
{
Console.WriteLine("Element not found in array");
}
Summary
- Linear Search iterates over the entire array, one element at a time, until the desired item is found
- Time complexity of Linear search is O(n)
- Binary Search works on a sorted array
- Binary Search eliminates half of the elements with every step, making the search faster.
- Time complexity of Binary Search is O(logn)
Feature image source: https://www.pexels.com/@pixabay