Brands of cars. Debit card transactions in a day. A shopping list. All these represent a list or collection of things that can be grouped into a particular category or type.

Type	Value
Car Brands	“Honda”, “Toyota”, “Hyundai”, “Ford”, “Audi”
Debit Card Transactions	“$25”, “$45.67”, “$140”, “$10”
Shopping List	“Jeans”, “Groceries”, “Books”

These all types can also form the data that a computer program works upon. For instance, whenever you do a self-checkout at Walmart, the software that calculates the total due amount would first need the details of the items that you bought from the store. But how does a computer store and process such a list of items?

Here is where data structures come into play, and when it comes to a collection of items, Array is a simple and powerful data structure that stands out.

Definition of Arrays

Array is a type of data structure that stores a collection of items at contiguous memory locations. What does contiguous memory locations mean? Well, think of the computer memory as a collection of blocks, where each block has its unique address (001, 002, 003…..and so on)

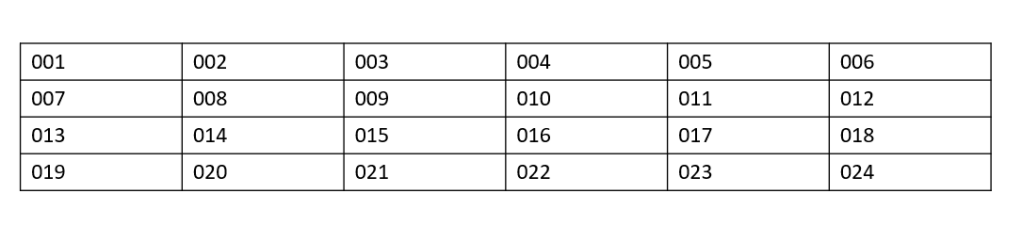
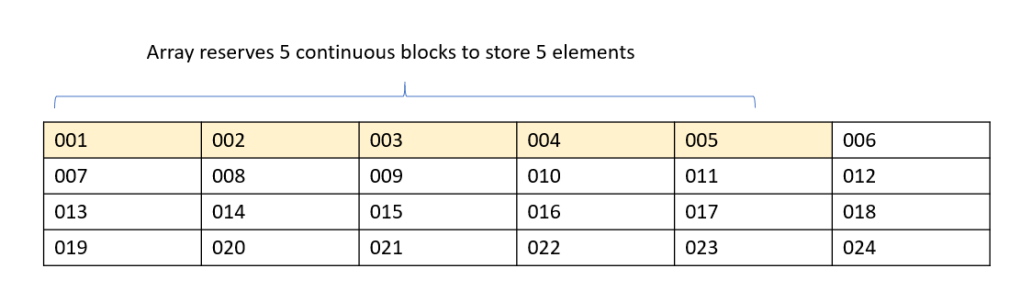
Each block can be considered as a small storage unit which can hold one element. An array of 5 elements will occupy 5 consecutive blocks in the memory to store its data.

Each memory location is referenced by an index. The first position would be index 0 (and will also be the address of the array). The subsequent indexes would be 1,2,3 and so on.

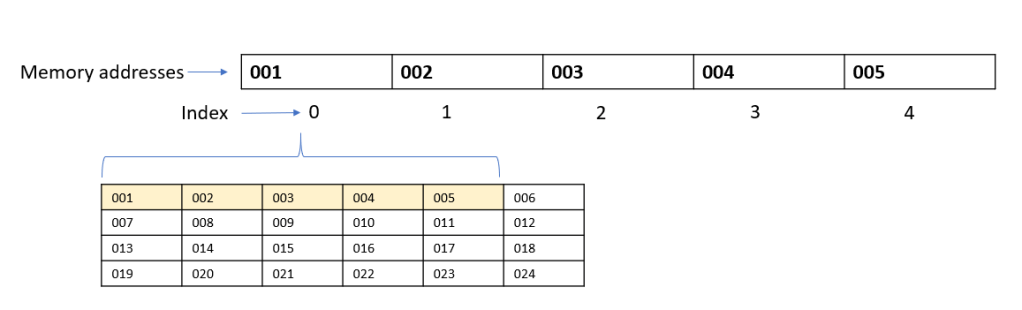
And now if we want to store the values of car brands in our array, the computer will store them as follows:

Delcaring and initializing arrays

An array is usually declared in a programming language as follows:

//This is C# syntax
//Other programming languages may declare arrays a bit differently

int[] arr = new int[5] // an array to store 5 integers

string[] cars = new string[5] // an array to store 5 car brands

The square brackets [] indicates the compiler that we are declaring an array, and the number inside the square brackets [5] indicates that the array would contain five elements. We need to specify the number of elements in advance, so that the array can reserve the appropriate block of memory to store the elements. (There are collections like dynamic arrays and Array lists which do not require us to specify the number of elements in advance, but these topics are not in the scope of this article)

By using indexes, we can add data to the array:

cars[0] = "Toyota" //adding Toyota to position 1
cars[1] = "Honda"
cars[2] = "Audi"
cars[3] = "Mercedes"
cars[4] = "Ford"

Reading From an Array

We can read data from the array using indexes as well

string myCar = cars[1] //read the car at index 1 or position 2 in the array

Reading from arrays is a fast operation. The computer knows the address of the array, and if we know the position of the value to be read, the computer can do a quick calculation of (address + position) and jump to that address. This is the power of storing items at contiguous locations.

In laymen terms, to read an element from an array takes only one step -> the computer calculating the address of the desired element and reading it.

In computing terms, the read operation of an array would always take constant time, which can be represented as O(1) or order of 1.

Inserting elements into an Array

Data can be inserted into an array, again by using indexes.  The easiest way to add data to the array is at the end of the array.

In the above example, we can add an element at index 5 as follows:

cars[5] = "Hyundai"

We can also insert data in the middle and beginning of an array. But this operation is a bit inefficient as we need to shift data in the array to accommodate for the newly added element. For example, if we have to insert “Kia” at index 2, then we would need to move Audi to index 3, Mercedes to index 4 and so on:

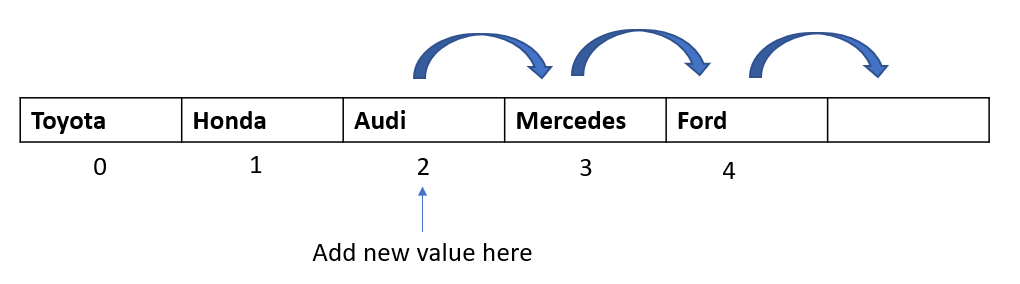
The worst case would be to enter data in the beginning of the array, as we would have to move all values one index to the right:

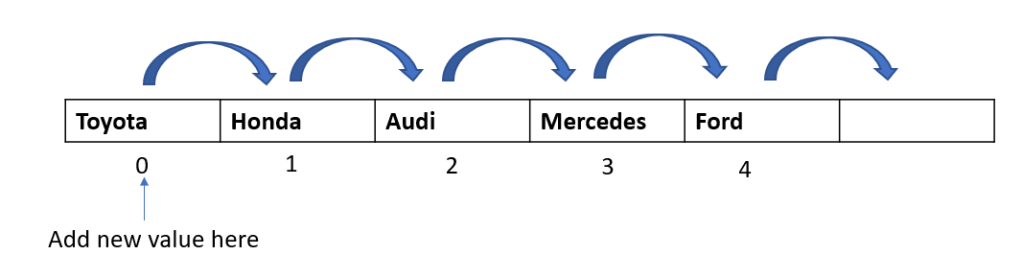
In laymen terms, we can say that for an array of “n” elements, the worst case scenario would be to insert an element in the beginning, which would require us to shift elements “n” times before the new element can be inserted.

In formal or computing terms, this operation would take “n” time in the worst case scenario and this complexity can be represented as O(n) or order of n.

Deleting from an Array

Deletion would be similar to insertion. Deleting an element from the end of the array would be the easiest. But, if we wish to delete an element from the beginning or middle of the array, then we need to shift all the remaining elements one position to the left.

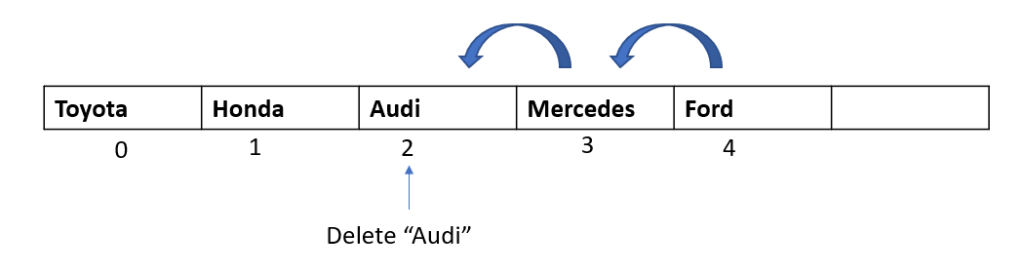
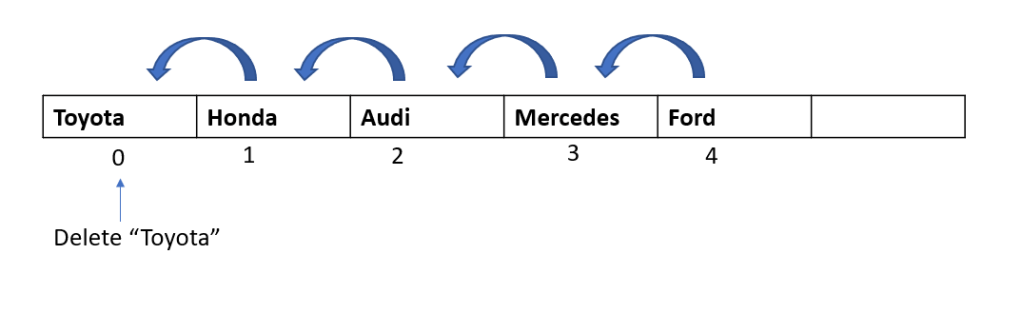
Like insertion operation, the worst case scenario for deletion would be the case when we want to delete an element from the beginning and we will have to shift all elements one index to the left. Thus, the complexity of the deletion operation is O(n) as well.

Searching an Array

If we want to search an element in an array (that is, we do not know the index of the element before hand), then we would need to traverse the array until we find that element. The best case scenario would be that the first element in the array is the element that we are looking for. The worst case would be the case where the element is in the end. In such a case we will have to traverse the entire array to get to the last element. Again, the complexity of searching an element in the worst case would be O(n).

Another worst case scenario would be that the element that you wish to search does not exist in the array at all. That would also lead to a full traversal of the array leading to a complexity of O(n).

Summary

• Arrays are data structures which store a collection of items in contiguous memory locations
• Each element in an array is assigned an index. The first element will start from index 0
• Elements can be added and removed from the array using indexes
• Reading operation takes constant time O(1) and this is one of the strengths of an array
• Insertion, deletion and search operations take O(n) time in the worst case